在统计学和金融领域中，期望与方差是两个重要的概念。期望代表了一个随机变量的平均值，而方差则表示了其波动性。准确理解和应用这些概念对于数据分析和风险管理至关重要。本文将深入探讨期望与方差的定义、计算方法及其在实际应用中的意义。

期望的定义与计算方法

期望是衡量一个随机变量取值可能性的平均值，用于描述随机变量的中心趋势。通过对每个可能取值乘以相应概率的加权平均来计算期望。期望是数据分析中常用的统计指标，可以帮助我们了解变量分布的特征。

方差的定义与计算方法

方差是描述随机变量离散程度或波动性的指标。它衡量了随机变量取值与其期望之间的偏离程度。方差的计算方法是将每个取值与期望的差平方后再乘以相应概率，然后将所有结果相加。方差是用来度量数据集的分散程度，可以帮助我们评估风险和预测未来走势。

期望与方差的关系

期望和方差是统计学中两个重要的概念，它们之间存在一定的关系。具体来说，方差可以看作是随机变量与其期望之间差的平方的期望值。也就是说，方差是对数据分布的离散程度进行量化的指标。

期望与方差的重要性

期望与方差在统计学和金融领域中具有广泛的应用价值。例如，在股票市场中，我们可以使用期望和方差来衡量股票收益的平均水平和波动性，从而评估股票的投资价值和风险。在工程和物理学中，期望与方差可以帮助我们预测和优化系统的性能。

期望与方差的计算示例

通过一个简单的数学示例，我们将演示如何计算期望和方差。假设有一个骰子，我们希望计算出它的期望和方差。通过对每个可能取值与其概率的加权平均，我们可以得到骰子的期望值为3.5，方差为2.92。

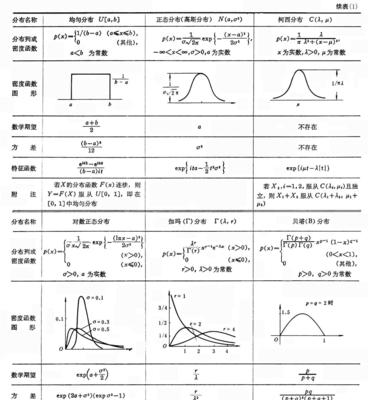
期望与方差的应用举例：投资组合

在金融领域中，投资组合是指将不同的资产按一定比例进行组合以达到最佳风险收益平衡的策略。期望和方差可以帮助我们评估不同资产组合的风险和收益，并找到最优的投资组合。

期望与方差的应用举例：风险管理

在风险管理领域中，期望和方差被广泛用于评估和控制风险。通过计算资产或投资组合的期望和方差，我们可以确定其风险水平并制定相应的风险控制策略。

期望与方差的应用举例：可靠性工程

在可靠性工程中，期望和方差被用于衡量系统的可靠性和稳定性。通过计算系统故障发生的期望次数和方差，我们可以预测系统的寿命和优化维护策略。

期望与方差的应用举例：产品质量控制

在质量控制过程中，期望和方差可以帮助我们评估产品的平均质量水平和质量波动性。通过控制生产过程的期望和方差，我们可以提高产品的一致性和质量稳定性。

期望与方差的局限性和扩展

尽管期望和方差在统计学和金融领域有着广泛的应用，但它们也存在一些局限性。例如，期望和方差都对极端值敏感，不适合处理非对称分布和离群点。为了克服这些问题，人们提出了一些扩展方法，如偏度和峰度等。

偏度与峰度：期望与方差的补充指标

偏度和峰度是期望与方差的补充指标，用于描述数据分布的偏斜程度和峰态。偏度衡量了数据分布的不对称性，而峰度则描述了数据分布的尖锐程度。通过结合偏度、峰度与期望、方差，我们可以更全面地理解数据的分布特征。

实际数据分析中的案例研究

通过一个实际的数据分析案例，我们将展示如何运用期望与方差的概念来解读和分析数据。以某公司的销售数据为例，我们将计算销售额的期望和方差，并通过对比不同产品线的期望和方差，帮助公司制定销售策略。

金融风险管理中的应用案例

在金融风险管理领域，我们将通过一个实际的案例研究来展示期望与方差在风险评估和投资决策中的应用。通过计算不同投资组合的期望和方差，我们可以评估投资组合的风险水平，并找到最佳的资产配置策略。

期望与方差公式的推导

本节将详细介绍期望与方差的计算公式的推导过程。通过数学推导，我们可以更深入地理解期望和方差的定义及其计算方法。

期望和方差是统计学中两个重要的概念，在数据分析、金融领域和风险管理中有着广泛的应用。准确理解和应用期望与方差的概念对于数据分析师、金融专业人士和风险管理者来说至关重要。希望通过本文的介绍，读者能够对期望与方差有更深入的理解，并能够灵活运用于实际问题中。