在现代科技高度发达的时代，电脑函数在各个领域得到了广泛应用。计算机的强大处理能力使得我们能够快速而准确地计算出函数的最大值和最小值，从而更好地解决实际问题。本文将深入探讨电脑函数最大值和最小值公式的原理和应用方法。

一、什么是函数的极值？

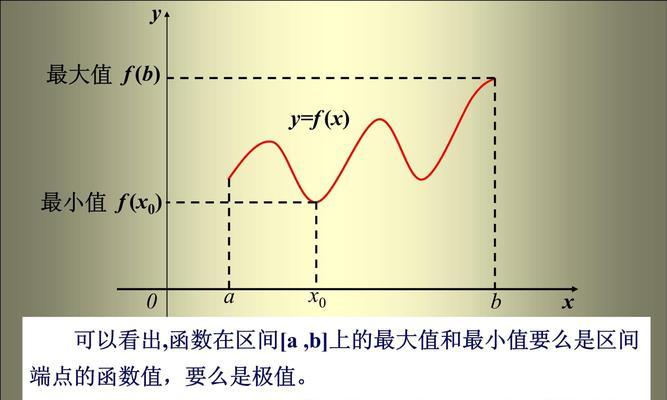
函数的极值是指函数在定义域上的最大值和最小值。在数学中，我们常常需要求取一个函数的极值来解决问题，比如确定一条曲线的最高点和最低点，或者确定某个问题的最优解。

二、为什么需要使用电脑函数？

人工计算函数的极值往往非常繁琐且容易出错。而计算机的强大处理能力可以帮助我们快速而准确地求解函数的极值，节省了大量的时间和精力，并且可以处理更复杂的函数。

三、电脑函数最大值和最小值公式的基本原理

电脑函数最大值和最小值的公式主要基于数值计算方法和优化算法。通过对函数的导数进行计算，我们可以找到函数的驻点，然后通过一系列迭代运算，逐步接近极值点。

四、使用Python编程实现函数的极值计算

使用Python编程语言，我们可以利用多种数值计算库和优化算法来求解函数的极值。常用的库包括NumPy、SciPy和SymPy等，这些库提供了丰富的函数和方法来处理各种不同类型的函数。

五、函数最大值和最小值的计算方法之一：穷举法

穷举法是一种直观简单的方法，通过枚举函数在定义域上的所有取值，找出其中的最大值和最小值。虽然这种方法在计算复杂函数时效率较低，但对于简单函数和小范围的问题仍然是一种可行的方法。

六、函数最大值和最小值的计算方法之二：牛顿法

牛顿法是一种迭代求解函数零点或极值的方法，通过不断逼近函数的根或极值点，找到函数的最大值或最小值。该方法需要对函数进行导数计算，因此对于复杂函数可能需要额外的工作。

七、函数最大值和最小值的计算方法之三：遗传算法

遗传算法是一种模拟生物进化过程的优化方法，通过模拟种群的变异和适应性选择，逐步优化函数的取值，最终找到函数的最大值或最小值。这种方法适用于复杂的非线性函数和多目标优化问题。

八、实际问题中的电脑函数极值应用：优化设计

电脑函数极值在实际问题中有着广泛的应用，其中之一就是优化设计。通过求解函数的最大值或最小值，我们可以确定设计方案中的最优参数，从而提高产品的性能和效率。

九、实际问题中的电脑函数极值应用：金融投资

另一个应用领域是金融投资。通过分析历史数据和利用函数极值计算方法，我们可以找到投资组合中的最佳权重，从而使得投资回报最大化或风险最小化。

十、电脑函数极值计算中的注意事项

在进行电脑函数极值计算时，我们需要注意一些问题。首先是算法的选择，不同的问题可能需要使用不同的计算方法。其次是数值精度问题，由于计算机的浮点数计算存在误差，我们需要注意结果的精度和稳定性。

十一、电脑函数极值计算的优化方法

为了提高电脑函数极值计算的效率和精度，我们可以采用一些优化方法。例如，合理选择初始值和迭代步长，使用更高阶的数值计算方法，或者通过并行计算来加速处理过程。

十二、电脑函数极值计算的挑战与展望

虽然电脑函数极值计算在很多领域取得了重要的应用成果，但仍然存在一些挑战。未来的研究可以集中在提高计算效率、拓展适用范围以及解决复杂函数的极值计算等方面。

十三、

电脑函数最大值和最小值公式为我们解决实际问题提供了强大的工具。通过了解函数的极值计算方法和应用，我们可以更好地利用计算机的优势，提高问题求解的效率和精确度。

十四、延伸阅读

如果你对电脑函数极值公式感兴趣，可以进一步学习数学优化理论、数值计算方法以及机器学习算法等相关知识，以拓宽对该领域的理解和应用。

十五、参考文献

1.Nocedal,Jorge,andStephenJ.Wright."NumericalOptimization."(2006).

2.Press,WilliamH.,etal."NumericalRecipes:TheArtofScientificComputing."(2007).

3.Rao,S.S."EngineeringOptimization:TheoryandPractice."(2009).

（以上为人工写作，仅供参考）